Когда идет изучение булевой алгебры, нужно запоминать таблицу истинности для быстрых решений задач. А что если не получается запомнить таблицу истинности? Что если абстрактные примеры не помогают? На помощь приходят принципиальные схемы!
Главное правило электрических цепей — электрический ток идет только по замкнутой цепи. Теперь рассмотрим примеры.
Конъюнкция (Логическое И)
Допустим есть схема с выключателями (SA1, SA2) и лампочкой (HL1). Они все последовательно соединены с батарейкой GB1.
Чтобы лампочка загорелась, нужен электрический ток. То есть, цепь должна быть замкнута.
Если лампочка HL1 загорается, значит в таблице A&B ставим 1.
В первом примере оба выключателя выключены. Значит электрического тока в цепи нет, и лампочка не загорается.
| A (SA1) | B (SA2) | A&B (HL1) |
| 0 | 0 | 0 |
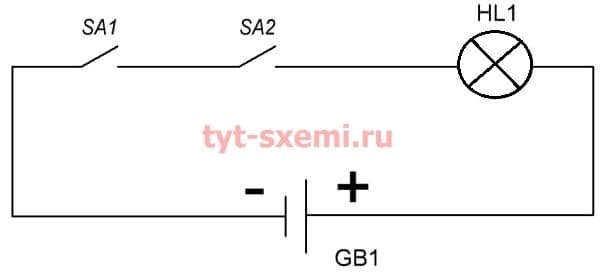
Во втором примере, если мы замыкаем выключатель SA1, то ток все равно не пойдет по цепи, так как второй выключатель SA2 все еще разомкнут. И лампочка не загорается. Электрический ток при последовательном соединении имеет только один путь. А если на пути разрыв, то и потока электронов не будет.
| A (SA1) | B (SA2) | A&B (HL1) |
| 1 | 0 | 0 |
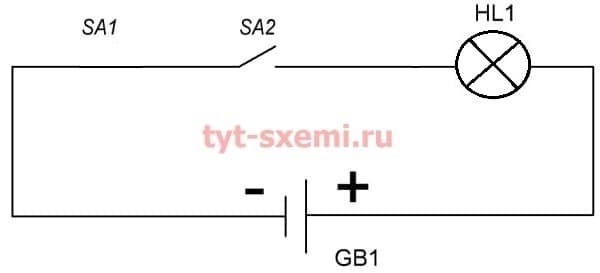
А в третьем примере лампочка загорается. Потому, что оба выключатели замкнуты, и ток по цепи течет.
| A (SA1) | B (SA2) | A&B (HL1) |
| 1 | 1 | 1 |
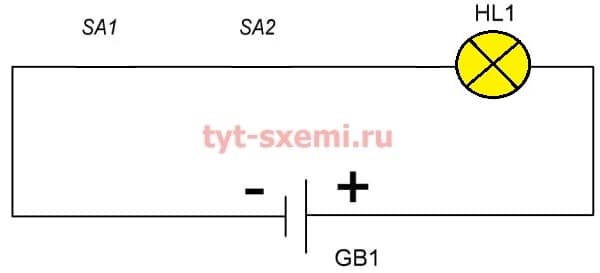
И этот пример демонстрирует правило:
| A | B | A&B |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (Логическое ИЛИ)
С дизъюнкцией схема поменяет свой вариант. Теперь выключатели SA1 и SA2 подключены параллельно, а не последовательно.
В первом случае лампочка HL1 не загорается. Потому, что ни один из выключателей не замкнут.
Поэтому в таблица заполнена нулями.
| A (SA1) | B (SA2) | A||B (HL1) |
| 0 | 0 | 0 |
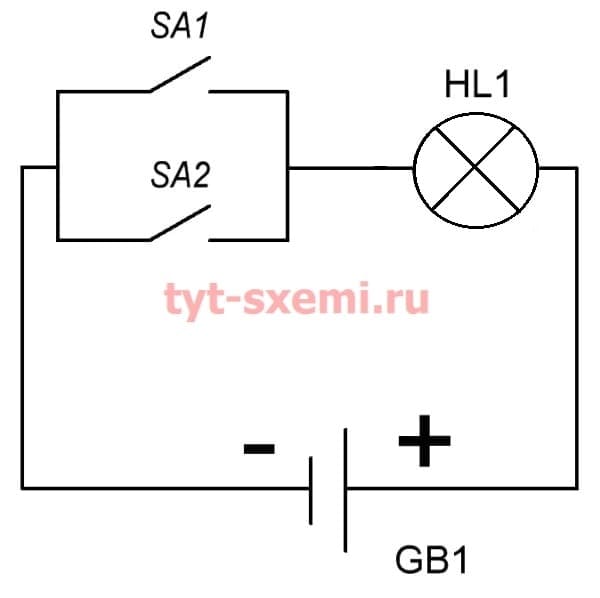
А что если SA2 замкнуть? Тогда и лампочка загорится. При параллельном соединении у электрического тока будет несколько путей. И он пойдет по тому, где нет обрыва.
| A (SA1) | B (SA2) | A||B (HL1) |
| 0 | 1 | 1 |
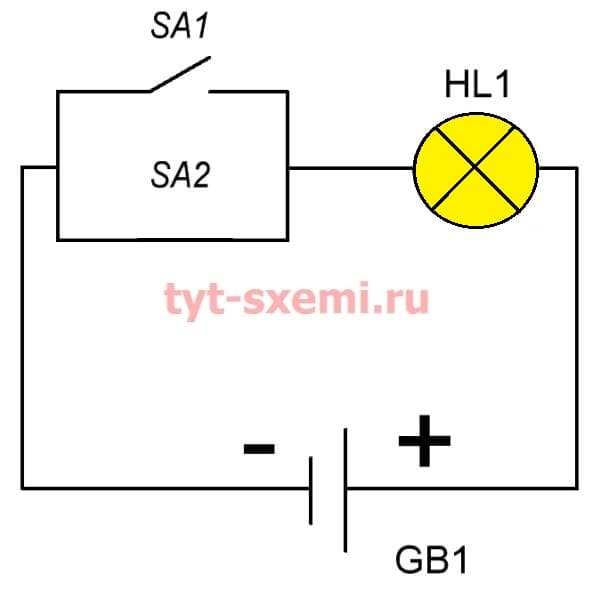
Замыкаем оба выключатели и происходит тоже самое. Лампочка горит.
| A (SA1) | B (SA2) | A||B (HL1) |
| 1 | 1 | 1 |
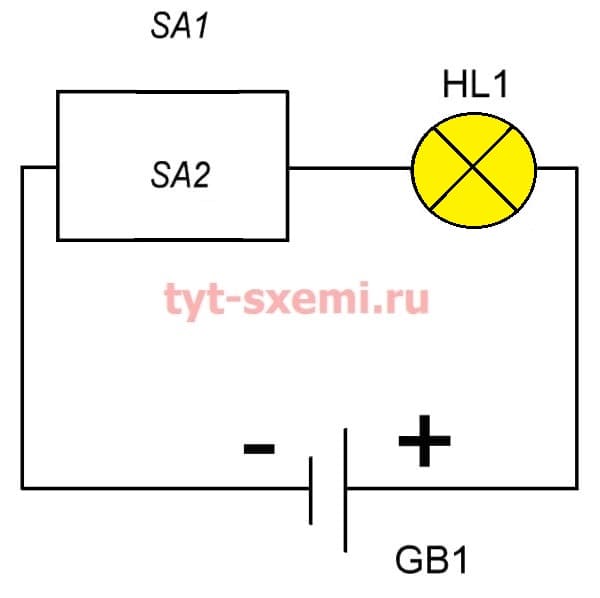
Если мы выключим SA1 и оставим SA2 включенным или наоборот, то лампочка все рано будет гореть, польку у электрического тока уже будет два пути. И ему неважно, будет ли замкнуты оба выключателя, или только один. Главное правило, чтобы был замкнут хотя бы один выключатель.
Поэтому, такая операция называется ИЛИ:
| A | B | A||B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Отрицание (Логическое НЕ)
С отрицанием все проще. По сути, это обычный инвертор.
Или схема с одним выключателем.
Параллельно к лампочке HL1 подключим выключатель SA1.
| A (SA1) | ¬A (HL1) |
| 0 | 1 |
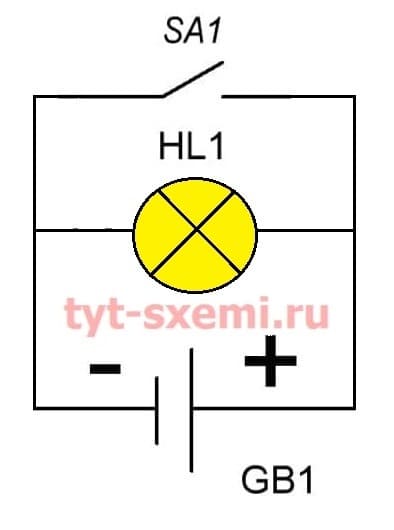
А если мы замкнем выключатель SA1, то лампочка погаснет. Почему? Потому, что электрический ток пойдет по наименьшему сопротивлению. А так как лампочка имеет большее сопротивление, чем провод, то через нее меньше пойдет ток, и она не загорится.
| A (SA1) | ¬A (HL1) |
| 1 | 0 |
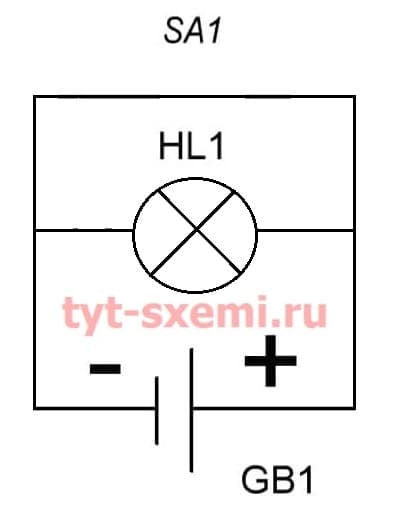
| A | ¬A |
| 0 | 1 |
| 1 | 0 |
Добавить комментарий